
Nuclear fission is a process in which a nucleus divides into two (or sometimes even three) lighter nuclei. Other particles (neutrons, for example) and electromagnetic radiation (gamma rays) are generally released as well. Fission can occur spontaneously but is more often induced.
The most common fission reaction occuring in nuclear reactors is:
n + 235U → X + Y + (0-8)n + γ + excess energy
where X and Y denote the nuclei that the Uranium has divided to. These are called fission fragments (examples: 99Zr, 99Mo, 137Te, 140Xe, etc.) and have masses that almost sum up to the mass of the original Uranium nucleus (note that from 0 to 8 neutrons are released).
Animation of fission reaction: number of neutrons and gammas in every reaction can be different (requires Adobe Flash)
In the nuclear fission of Uranium, in average, 2.5 neutrons are produced, so the reaction leads to a multiplying number of neutrons in the system. Most of the fission fragments are radioactive, and on average, there are about five photons (gamma rays) emitted in a single reaction.
The animation illustrates the fission reaction n + 235U → 90Kr + 143Ba + 3n + 4γWhen a neutron is absorbed by the 235U nucleus, a 236U nucleus is formed, having such a high energy that the nucleons inside start oscillating vigorously and the nucleus elongates.
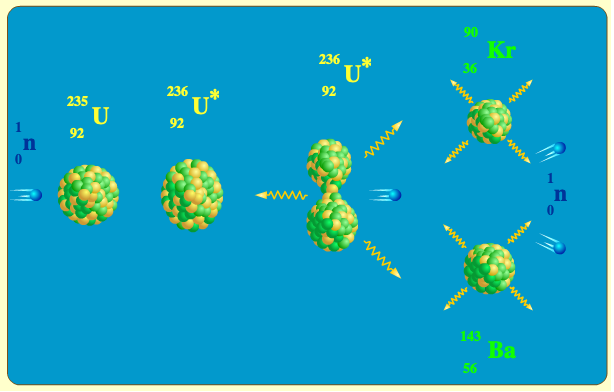
The energy released when a 235U undergoes fission is about 200MeV. This energy is the kinetic energy of the fission fragments (about 167MeV), neutrons (about 5MeV), and about 17MeV are released in the beta decays (in average, 3 decays per fragment). The remaining 7MeV is emmited as gamma rays.
Remember that the burning of a single carbon atom gives off only about 4eV of energy - some 50 million times less! The energy per molecule released by the explosion of TNT is also very small by comparison: about 18 million times smaller.
We've learned that in a typical fission reaction of 235U, around 2 neutrons are produced.
The number of individual fissions in a chain reaction is proportional to the number of fissionable nuclei in the material. Neutrons produced by fission can initiate another fission if they are absorbed by a fissile nucleus. But fission neutrons can be absorbed by other type of a nuclei, or even escape from the material. Hence, the probability that fission will occur is less than 1. However, there are some ways to increase this probability.
Neutrons released in fission have about 1-2 MeV of energy. Such fast neutrons have a very low probability of causing fission of 235U and so these neutrons will pass by many, many nuclei before being absorbed by one and inducing fission. One solution is to slow them down, i.e. make sure that they have relatively small energies (a fraction of 1eV). You can think of the higher probability as arising from the fact that slow neutrons spend a longer time in contact with the Uranium nucleus. We call such neutrons thermal neutrons, because their kinetic energies are close to the kinetic energies of the molecules in the air around us. To slow down neutrons in a fission reactor for example, one fills the voids between the fissile material with a so-called moderator, for example water or graphite.Another method of incresing the probability of neutron capture is to surround the fissile material with a neutron reflector, that will scatter the neutrons back to increase the number of collisions. In particular, beryllium, graphite and steel are common reflector materials.
Moreover, some neutrons will encounter nuclei that absorb neutrons. In the case of thermal neutrons such efficient absorbers include nuclei of boron, cadmium and gadolinium. Fast neutrons are strongly absorbed by the most common isotope in natural uranium, 238U, producing fissionable 239Pu and 240Pu. Therefore, one must know the chemical and isotopic composition of amaterial in which we expect to observe a chain reaction. Will learn more about all these in the next section, dedicated to nuclear reactors.